Geometrická posloupnost je druh matematické posloupnosti, kde každý člen kromě prvního je stálým násobkem předchozího členu. Tento násobek se nazývákvocient geometrické posloupnosti a pro posloupnosti s nenulovými členy je roven podílu libovolného členu kromě prvního a členu předchozího.
Geometrickou posloupnost s nezápornými členy lze chápat jako zúžení exponenciální funkce na obor přirozených čísel (připouštíme však i základ 0 a 1) a proto i pro svou jednoduchost je jedním z nejdůležitějších typů posloupností.
Pro vyjádření n-tého členu geometrické posloupnosti s kvocientem q lze použít různé vztahy.
Rekurentní zadání
Geometrické posloupnosti lze definovat jako řešení lineární rekurentní rovnice 1. řádu s konstantními koeficienty:
Řešením lze zjistit vzorec pro libovolný člen:
První člen a1 má libovolnou hodnotu (je to tzv. počáteční podmínka), obecný vztah pro n-tý člen se dokáže snadno matematickou indukcí.
Zadání vzorcem pro n-tý člen
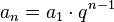 .
.
Pro případ 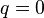 používáme
používáme  .
.
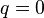 používáme
používáme  .
.Příklad
Například je-li  , pak několik prvních členů geometrické posloupnosti je: 2, 6, 18, 54, 162, 486 …
, pak několik prvních členů geometrické posloupnosti je: 2, 6, 18, 54, 162, 486 …
 , pak několik prvních členů geometrické posloupnosti je: 2, 6, 18, 54, 162, 486 …
, pak několik prvních členů geometrické posloupnosti je: 2, 6, 18, 54, 162, 486 …
Pro  se jedná o posloupnost 1, -1, 1, -1, ...
se jedná o posloupnost 1, -1, 1, -1, ...
 se jedná o posloupnost 1, -1, 1, -1, ...
se jedná o posloupnost 1, -1, 1, -1, ...
Součet prvních n členů geometrické posloupnosti se vypočítá (pro q≠1):
a pro q=1 samozřejmě (jedná se pak o konstantní aritmetickou posloupnost):
Tento zvláštní případ lze také dostat z předchozího vzorce limitním přechodem pro  .
.
 .
.
Vztahy platí v libovolném komutativním tělese, např. komplexních čísel.
Příklad
Součet prvních pěti členů posloupnosti z předchozího příkladu ( ) je:
) je:
 ) je:
) je:http://cs.wikipedia.org/wiki/Aritmetick%C3%A1_posloupnost
Aritmetická posloupnost je druh matematické posloupnosti, kde je stálý rozdíl mezi sousedními členy. Tento rozdíl mezi libovolným členem kromě prvního a předcházejícím členem se obvykle značí d a nazývá diference.
Aritmetickou posloupnost lze chápat jako lineární funkci definovanou v oboru přirozených čísel a proto i pro svou jednoduchost je jedním z nejdůležitějších typů posloupností.
Zobecněním je aritmetická posloupnost vyššího řádu (někdy též vyššího stupně), jejíž i-tý člen lze vyjádřit jako hodnotu nějakého pevného polynomu pro danéi. Řád aritmetické posloupnosti pak definujeme jako stupeň tohoto polynomu, přičemž posloupnost samých nul má řád -1.
V následujících vzorcích označuje  n-tý člen aritmetické posloupnosti a d její diferenci.
n-tý člen aritmetické posloupnosti a d její diferenci.
 n-tý člen aritmetické posloupnosti a d její diferenci.
n-tý člen aritmetické posloupnosti a d její diferenci.Rekurentní zadání
Zadání vzorcem pro n-tý člen
Vyjádření r-tého členu z s-tého
Součet prvních n členů
Příklad
Například je-li  a
a  , pak několik prvních členů aritmetické posloupnosti je: -5, -2, 1, 4, 7, 10, 13, …
, pak několik prvních členů aritmetické posloupnosti je: -5, -2, 1, 4, 7, 10, 13, …
 a
a  , pak několik prvních členů aritmetické posloupnosti je: -5, -2, 1, 4, 7, 10, 13, …
, pak několik prvních členů aritmetické posloupnosti je: -5, -2, 1, 4, 7, 10, 13, …





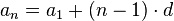


Žádné komentáře:
Okomentovat